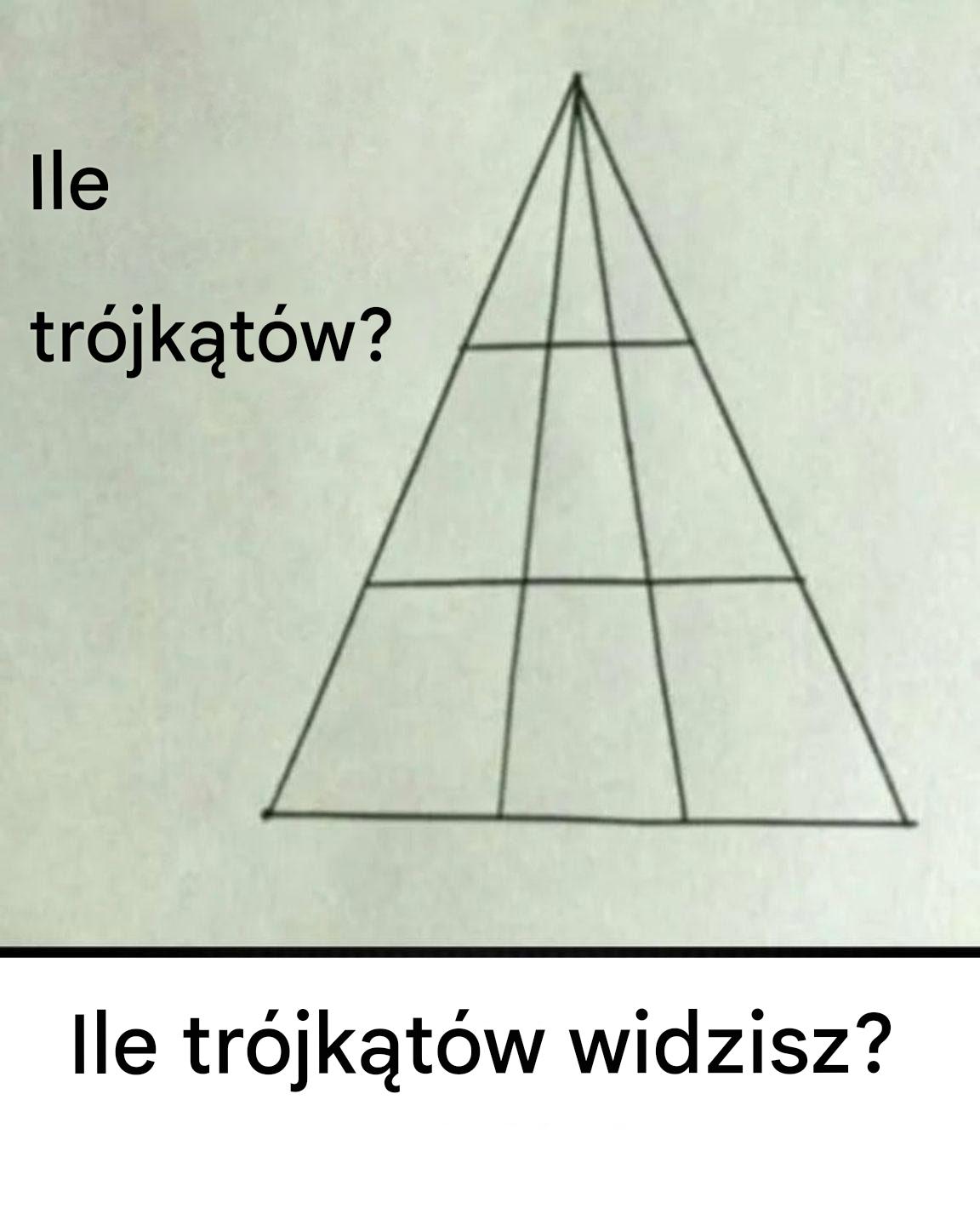
Ile trójkątów widzisz na tym obrazku?
Myślałeś, że znalazłeś właściwą odpowiedź, ale… ta słynna łamigłówka pozostawiła obojętnym niejednego doświadczonego oko! Na pierwszy rzut oka liczysz kilka trójkątów, a następnie dodajesz je, przechodząc przez „poziomy”. Proste? Nie do końca. Ta figura – duży trójkąt przecięty u podstawy trzema równoległymi liniami – kryje w sobie więcej kształtów, niż możesz sobie wyobrazić. Gotowy, aby uniknąć pułapki i zabłysnąć w kolejnym quizie o aperitifie? Postępuj zgodnie z instrukcją.
Pułapka ukrytego trójkąta.
Nasz mózg uwielbia dostrzegać małe, oczywiste trójkąty i… zapomina o dużych, utworzonych z połączenia kilku obszarów. W rezultacie niedoceniamy. W klasycznej konfiguracji (4 rzędy utworzone przez 3 linie równoległe do podstawy) poprawna odpowiedź to 27. Gdybyś
odpowiedział 26, najprawdopodobniej przegapiłbyś duży trójkąt złożony, często trójkąt z wierzchołkiem skierowanym do góry, rozciągający się na 3 poziomy, lub trójkąt „o szerokości połowy” z jednej strony.
Metoda krok po kroku: liczenie bez błędów

Wysokość 1 poziom: 10
Wysokość 2 poziomy: 6
Wysokość 3 poziomy: 3
Wysokość 4 poziomy: 1
Suma częściowa „w górę”: 10 + 6 + 3 + 1 = 20.
Dodaj trójkąty skierowane w dół, które powstają w wyniku zagnieżdżenia segmentów: 7.
Razem: 20 + 7 = 27.
Wskazówka dotycząca pamięci: myśl „20 na górze + 7 na dole”, a unikniesz klasycznego zapominania.
Magiczna formuła wyjaśniona w prosty sposób

Potrzebujesz eleganckiego skrótu? Dla dużego trójkąta podzielonego na n wierszy liniami równoległymi do podstawy (tu n = 4), możemy zastosować następujący wzór:
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Zastosowano an = 4:
T = 4 × 6 × 9 ÷ 8 = 27